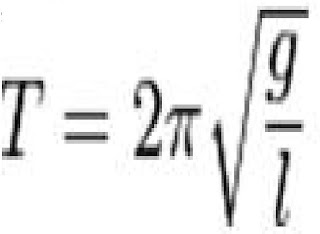COLEGIO NACIONAL “CÉSAR ANTONIO MOSQUERA”
ESPECIALIDAD DE FÍSICO MATEMÁTICO
INFORME DE LABORATORIO DE FÍSICA
PRÁCTICA N º2 ASIGNATURA: Mecánica
NOMBRE: Yomayra Carolina Pusdá Velasco
Curso: 2º Bachillerato Físico Matemáticas
TEMA: medida de la aceleración de la gravedad con el péndulo reversible
Fecha: 2010-02-08
GRUPO Nº: 3
OBJETIVO: Determinar la aceleración de la gravedad con el péndulo reversible.
ESQUEMA Y REFERENCIAS DE LO DIPOSITIVOS:

2. Varilla de soporte
3. Nuez varilla de 10 cm
4. Brazo de balanza
5. Espigas para brazo de balanza
6. Cronómetro papel milimetrado
Lápiz.
TEORÍA Y REALIZACIÓN:

Un péndulo de Kater es un ejemplo
de péndulo compuesto o físico, por ello, es
un cuerpo rígido que puede oscilar
libremente alrededor de un eje horizontal,
que no pasa por su centro de masa.
Hemos comprobado experimentalmente que hay un punto en el que el péndulo tiene el mismo periodo, oscile de O o de S. Esto equivale a decir que hay dos valores de a que en esta expresión nos van a dar el mismo periodo, ya que el momento de inercia IG, y la masa del sistema son constantes, y por tanto lo único que varía es la distancia del centro de gravedad al eje de oscilación.
Período de tiempo de oscilación doble(T) es el tiempo que emplea el péndulo en efectuar una oscilación doble.
Para estas determinaciones se emplean péndulos reversibles, es decir, péndulos que pueden oscilar primero alrededor de un eje y luego alrededor de otro.
PROCEDIMIENTO:
1.Metemos en los orificios de los extremos del brazo de balanza sendas espigas y suspendemos el sistema por una de ellas(punto de suspensión D1)
desviamos el sistema unos 2 cm y determinamos el período T1, midiendo el tiempo t1 invertido en dar 10 oscilaciones.
Luego suspendemos el péndulo por el oro extremo(punto de suspensión D2) Repetimos el cálculo.
Repetimos cada una de las medidas 3 veces y calculamos el valor medio de de ls correspondientes períodos T.
Medimos la distancia interna a entre las es espigas, que es igual a la suma de S1 y s2, de las distancias desde los puntos de suspensión D1 y D2 al centro de gravedad S( a= s1 + s2 ),
2.vamos acercando la segunda espiga (punto de suspensión D2) poco a poco (2 cm) al centro de gravedad, mientras que mantenemos el otro en su sitio inicial (D1) y repetimos y repetimos lo del apartado 1.
Llevamos los valores encontrados t1, T1,t2, T2 y a la tabla:
Dibujamos un diagrama con los valores de T en función de los valores de a. Determinamos el valor de las coordenadas del punto de corte (T, l).
Hallamos la longitud equivalente del péndulo y su correspondiente período.
Calculamos, a partir de la fórmula del del período del péndulo matemático, la aceleración del la gravedad:

En donde l y T son los valores de las coordenadas del punto de corte del diagrama.
REGISTRO DE DATOS Y CÁLCULOS:

CUESTIONARIO Y CONCLYSIONES:
1.- ¿qué es el péndulo reversible? Un péndulo de Kater es un ejemplo
de péndulo compuesto o físico, por ello, es
un cuerpo rígido que puede oscilar
Libremente alrededor de un eje horizontal,
que no pasa por su centro de masa.
2.-¿Con que valores podemos determinar la aceleración de la gravedad?
Con el período y la longitud.
CONCLUSIONES:
Tomados los valores de los tiempos pudimos determinar los períodos y mediante la gráfica determinamos los valores del período y la longitud una vez obtenidos estos valores calculamos la aceleración de la gravedad.



 la aceleración angular
la aceleración angular